wolfram mathematica 10 中文破解版v10.3

mathematica 10是一款科学计算软件，也是使用范围最为广泛的数学软件之一，现在已经广泛使用于航空航天、大型工程、金融、教育教学等等各种领域。它能够非常好的结合数值和符号计算引擎、文本系统、图形系统、编程语言、以及一些应用程序的高级连接，使得它的各方面的计算能力大大增强，成为世界上通用计算系统中最强大的系统，并且其中很多的功能在相应的领域处于世界非常高的地位和水准。软件学堂提供的是mathematica 10破解版，并且还是中文版的哦！

安装破解教程

1、在本站的百度网盘资源上下载好软件安装包，将其解压好，然后再将“Mathematica_10.3.0_Chinese_WIN.zip”压缩包解压，双击运行里面的“setup.exe”，选择简体中文，点击“确定”。

2、连续一直点击“下一步”，直到软件安装完成，中间可以选择软件的安装目录。


3、软件安装完成，点击“完成”。

4、软件会自动打开，然后提示激活，我们选择“其他方式激活”-“手动激活”。


5、然后便可以看到你的“Math ID”号。

6、使用快捷键“windows+r”，会出现运行框，输入“cmd”，点击“确定”。

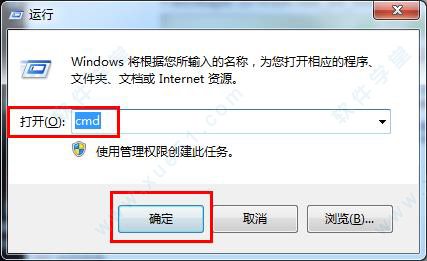
7、然后将“注册机Keygen.rar”压缩包里面的注册机“Mathematica_10.3.0_Keygen.exe”直接拖入弹出来的界面中，然后回车。

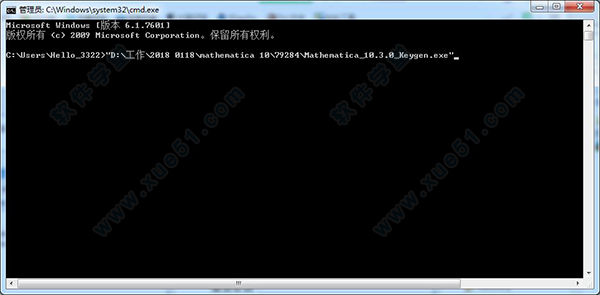
8、然后再将软件激活页面的“Math ID”号复制粘贴进去，回车。

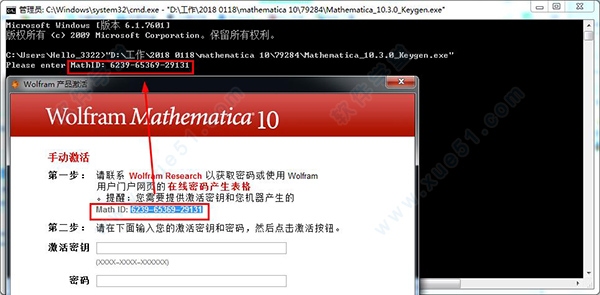
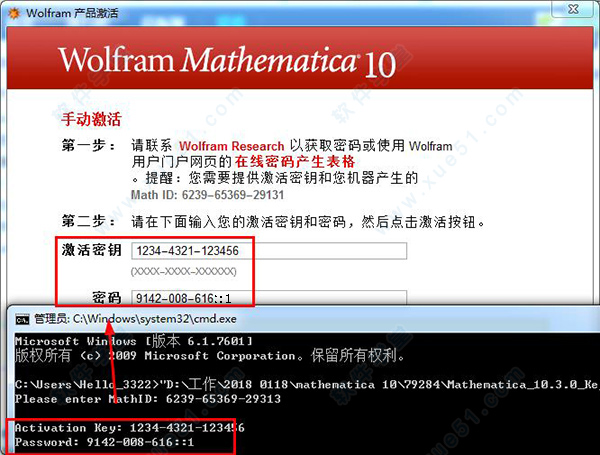
9、便会出现激活密钥和密码，将激活密钥的密码输入到软件的激活页面，点击“激活”，便可激活成功。

10、激活成功后软件会自动弹到“许可协议”界面，勾选“我接受该协议的条款”，点击“确定”。

11、产品注册，可以不用注册，点击“稍后注册”。

12、然后软件便会打开，以后便可以无限制的使用了。

使用指南

一、几种括号的含义
[]，所有的函数体都用方括号
{}，列表（list），这是软件中最重要的数据结构
()，就是普通的括号，用于改变优先级
二、数值近似，常量
轻易不显示分数、函数等的数值近似解，如果非要显示，就要使用显式的方法：N[1/3,10]，上式和1/3 //10效果一样，都是求出1/3的前10位小数。//后面会讲到，它是一个后缀用法。
内置的常量有：Pi，E，I，GoldenRatio分别为圆周率、自然对数底、虚数单位、黄金分割率。
可以直接输入希腊字母等特殊符号。两种方法，第一种：先按一下Esc，然后其英文拼法的第一个字母，基本就都联想出来了。有一些符号，还有缩写输入法。比如，输入α的方法：Esc-a-Esc；第二种，用转义符号\，差不多所有特殊符号都是用[]括起来的，比如α，输入方法：\[Alpha],大写的希腊字母前加Capital，比如大写α，输入方法：\[CapitalAlpha]
三、解代数方程
数学上的等号是==，=是赋值。
函数是Solve，给出方程（组）和变量（组）：
Solve[2x^2-3x+6==0,x]
Solve[{2x-3y==0,4x-7y==0},{x,y}]
不要解析解，要数值解，使用NSolve，用法完全类似。
四、解微分方程
一阶导数可以用y’[x]表示，二阶可用y’’[x]表示。基本用法：
DSolve[y’’[x]+y[x]==0,y[x],x]
DSolve[{y’’[x]+y[x]==0,y[0]==1,y’[0]==0},y[x],x]
五、二维绘图
基本绘图函数是Plot：
Plot[x*Sin[x],{x,-1,2},PlotStyle->Red]
Plot有大量属性可供配置，查看所有属性：
Options[Plot]
这些属性，有些能够望名知意，有些不能。不管能不能，建议使用?，查一下文档用法。其实在绘图后，会根据上下文联想出所有可供配置的选项的，一个个的去尝试即可，不必记住这么多的命令用法。不过，记住一些常用的配置选项还是有好处的，就是能够保证绘图的统一性。每次都通过点鼠标根据上下文尝试做出来的图，除非记录下来每次的操作，不然每次都不一样，而这在一些应用下是不可饶恕的。其中，比较重要的有：
AxesOrigin, Ticks, AxesLabel, PlotStyle, AspectRtio, PlotRange, Frame, FrameTicks, Axes, Mesh, MeshStyle, ColorFunction

软件特色

一、现代技术计算的唯一选择
通过三十多年来的精心研发和不断探索，并在许多领域独树一帜，在当今技术计算环境和工作流程中表现卓著。
1、一个全面集成的大型系统
具有涵盖所有技术计算领域的将近 5,000 个内置函数——所有这些都经过精心制作，使其完美地整合在一起。
2、不仅仅是数字，也不仅仅是数学，内容包罗万象
基于三十多年来的持续开发，在所有技术计算领域表现卓著，包括网络、图像、几何、数据科学、可视化、机器学习等等。
3、不可想象的算法功能
在所有领域构建了前所未有的强大算法—许多算法都是使用 Wolfram 语言独特的开发方法和功能进行构建的
4、前所未有的高级
从超级函数到元算法，并且提供了可实现自动化并且日益完善的高级环境，使您的工作尽可能地高效。
5、整体达到工业强度
拥有跨越各个领域的强大的高效的算法，还是为提供工业强度而构建的，它的并行计算、GPU 计算等功能使其可以轻松处理大型问题。
6、易于使用的强大功能
凭借它的算法功能以及 Wolfram 语言的详细设计原理，创建了具有预测性建议、自然语言输入等的独特的并且易于使用的系统。
7、文档以及代码
使用 Wolfram 笔记本界面，使您可以快速整理包括文本、可运行代码、动态图形和用户界面等的丰富文档中的任何内容。
8、代码可读性强
使用直观的类似英文的函数名称和一致明了的设计，Wolfram 语言易于阅读、编写和学习。
9、得到最美观的结果
使用最先进的计算美学和设计原理，为你呈现最美观的结果；立即创建最顶级的互动可视化效果和出版物质量级别的文档。
10、超过十五万个范例
从 参考资料中心 的 150,000 多个范例，Wolfram 演示项目的将近 10,000 个开源演示项目和其他资源中获取帮助，开始着手任何项目。
11、即时现实数据
可以访问广博的 Wolfram 知识库，包括最实时的数千个领域的数据。
12、完美的云端集成
目前已经完美地集成于云端系统中；可在统一强大的云端桌面混合环境中进行分享、云计算以及更多功能。
13、与任意内容连接
为与任意内容连接而构建：文件格式（180 多种）、其他语言、 Wolfram Data Drop、API、数据库、程序、物联网和设备，甚至其自身分布等。
二、核心技术
1、WOLFRAM 语言
脱胎于它的基于知识的独特符号式语言，推动了软件系统的发展。
2、WOLFRAM 算法库
全球最大的算法集成网络，为其提供了博大精深的内置功能。
3、WOLFRAM 笔记本界面
独特的灵活的基于文档的界面，使您可以混合软件中的可执行代码、格式丰富的文本、动态图形和互动界面。
4、WOLFRAM ENGINE
实现 Wolfram 语言和软件的核心软件系统；跨越了各种各样的本地和云端计算环境。
5、WOLFRAM CLOUD
仅仅使用一个网页浏览器就可以运行它的架构技术。
6、WOLFRAM KNOWLEDGEBASE
推动 Wolfram|Alpha 的独特广博的持续更新的知识库，并为 Wolfram 产品提供了可计算的现实数据。
三、超过三十年的漫长历程
在软件第一版中引入的五百多个函数，仍然涵盖在最新版的软件中，而且总计已总增添了将近 4,500 种不同函数，以及众多具有远见卓识的重要创新思想。
1、1988 年革新
当它首次在 1988 年诞生时，它为技术计算带来了革命性的变化，由此每年都持续不断引入更多新函数、新算法和新思路。
2、远远超过数学
数学是它第一个大型应用领域；基于数学领域的成功经验，且系统性地扩展到了许多新领域，包括各种技术计算格式。
3、创新速度越来越快
在三十年多的时间里遵从快速革新的发展轨迹，使得在每个阶段都构建了许多强大的新功能。
4、在每个版本中都有新思想
的各版本更新不仅仅是一般的软件更新；每个连续更新的版本都是在新方向上对计算模式的一次重大发展，并且引入了重要的新思路。
5、您在第一版中学到的技巧仍然可以用
如果您使用过首版的，那么您在三十年前编写的代码仍然可用，并且能够在现今的大型系统中再度遇见其第一版的核心思想。
6、三十年多来的持续发展
忠实于它的核心准则和严肃的设计原理，持续发展并且集成了许多新功能和方法，而无需走回头路。

新功能：

一、数学结构
1、增强的代数计算
版本10在原有的强大代数计算能力上增添了更多的扩展和改善. 更快的实数多项式系统的符号解以及一般多项式系统的数值解首次使更多问题可以计算处理. 新的专用函数自动计算函数定义域、域值和周期性. 最终，新的矩阵测试、增强的矩阵求解器和更多的内部增强功能使线性代数比以往更加快捷和方便.
2、量纲变量
Wolfram 语言为上百个不同领域提供了可立即访问的精选公式. 对于量纲分析、热力学计算、随选货币转换、以及根据物理量查找既有公式能力的提供了全面综合性支持，Wolfram 语言使数量计算比以往更加简单和灵活.
3、增强的图和网络
版本10从整体框架支持混合图、多重图、三维图可视化和强大的计算能力，通过将其在 Wolfram 语言中的完全整合，使对图和网络的建模、分析以及合成比以往更加简单.
二、几何计算
1、符号几何
版本10对以几何区域为关键要素的几何计算增添了更广泛的支持. 几何区域可以通过使用如圆形等特殊区域、公式、包含单个区域集合的网格，或通过布尔组合和变换来创建. 许多标准属性可直接用于计算如隶属测试、测度（例：长度、面积、体积）、几何中心、最近点等所有区域. 区域还可以用作包括最优化、代数方程求解、积分和偏微分方程求解等许多高级求解器的规范.
2、已命名 & 公式区域
版本10增添了对基础和基于公式的几何区域的完全支持. 基础区域为通用并且容易指定. 公式区域很灵活并且具有很强的描述能力. 基础和公式区域通常可对任意维数计算精确或近似解或涉及参数的结果. 基础和公式区域完全支持几何区域框架，其中包括计算属性（面积、最近点等）、作为解决器（最优化、求解 PDE 等）的输入以及离散化.
3、基于网格的区域
版本10增添了对基于网格的几何区域的完全支持. 基于网格的区域可被明确指定或从点的列表、图形或其他区域自动生成. 基于网格的区域有足够的灵活性逼近任何其他区域并支持几乎所有操作的快速算法. 基于网格的区域对包括计算属性（面积、最近点等）和用于求解器（积分、求解 PDE 等）的输入在内的几何区域框架有着完全支持.
三、机器学习
1、高度自动化的机器学习
从如 Predict 和 Classify 等高度自动化函数到基于特定方法和诊断的函数，版本10引入了范围广泛的集成机器学习能力. 函数适用于包括数值、分类、文本和图像在内的多种数据类型，以简单的方法让所用使用者执行最高端的机器学习. 可以执行例如文本分类、图像识别、通用数据分类等广泛任务.
2、内置分类器集合
版本10 中包含多种用于机器学习任务的系列预训练模型. 其中包括出现在数据科学中基于文本任务的模型，如垃圾邮件检测、语言检测或社会媒体主题识别，以及如旗帜识别的基于图像的模型.
3、自动时间序列分析
版本10可以对整套时间序列过程进行完全自动化的拟合和诊断处理，这使得时间序列建模成为研究的日常工具. 时间序列建模已被进一步深化，包括自回归条件异方差（ARCH）和广义自回归条件异方差（GARCH）过程，以及标准时间序列模型的向量值形式. 包括模拟、估计和属性计算等，在整个时间序列模型框架上有着大幅度的增强.
四、地理计算
1、地理可视化
Wolfram 语言中引入了制作地图的 GeoGraphics，它是强大图形功能的扩展. GeoGraphics 提供了对地图投影、缩放选择（从地球整体到米尺比例）、地图样式（街道地图、地形图......）等完全自动化和自由操作. GeoGraphics 引入了适用于地球表面（例如用于导航的测地线或恒向线）的新型地理学元素并通过新型 Entity 框架对 Wolfram|Alpha 中的大型地理学语料库进行综合访问.
2、与地理有关的属性
Wolfram 语言为轻松获取当前天气、天文数据、基于位置的城市和国家的知识提供许多方便的函数，并且如 GeoGraphics 等强大的地理可视化函数整合在一起. 对扩展的区域、近期和历史地震数据以及太阳和月亮位置的整体性支持的同时，Wolfram 语言为您提供了处理地理数据所需的全部工具.
3、基于实体的地理计算
Wolfram 语言中引入了完整的地理信息系统（GIS）. 其中集成了用于地图构建的强大的新的 GeoGraphics 函数，访问 Wolfram|Alpha 中大量语料库信息的新 Entity 框架，以及增强的大地测量学的计算功能. 使得无论使用任何类型的数据，都可以构建任意制图投影中使用的各种地图并包括任意计算结果的表示.

基本运算

a+
数学实验(第2版)
b+c 加
a-b 减
a b c 或 a*b*c 乘
a/b 除
-a 负号
a^b 次方
数字的形式
256 整数
2.56 实数
11/35 分数
2+6I 复数
常用的数学常数
Pi 圆周率，π=3.141592654…
E 尤拉常数，e=2.71828182…
Degree 角度转换弧度的常数，Pi/180
I 虚数，其值为 √-1
Infinity 无限大
指定之前计算结果的方法
% 前一个运算结果
%% 前二个运算结果
%%…%(n个%) 前n个运算结果
%n 或 Out[n] 前n个运算结果
复数的运算指令
a+bI 复数
Conjugate[a+bI] 共轭复数
Re[z], Im[z] 复数z的实数/虚数部分
Abs[z] 复数z的大小或模数(Modulus)
Arg[z] 复数z的幅角(Argument)
输出的控制指令
expr1; expr2; expr3 做数个运算，但只印出最后一个运算的结果
expr1; expr2; expr3; 做数个运算，但都不印出结果
expr; 做运算，但不印出结果
其常用数学函数
Sin[x],Cos[x],Tan[x],Cot[x],Sec[x],Csc[x] 三角函数，其引数的单位为弧度
Sinh[x],Cosh[x],Tanh[x],… 双曲函数
ArcSin[x],ArcCos[x],ArcTan[x] 反三角函数
ArcCot[x],ArcSec[x],ArcCsc[x]
ArcSinh[x],ArcCosh[x],ArcTanh[x],… 反双曲函数
Sqrt[x] 根号
Exp[x] 指数
Log[x] 自然对数
Log[a,x] 以a为底的对数
Abs[x] 绝对值
Round[x] 最接近x的整数
Floor[x] 小于或等于x的最大整数
Ceiling[x] 大于或等于x的最小整数
Mod[a,b] a/b所得的馀数
n! 阶乘
Random[] 0至1之间的随机数（最新版本已经不用这个函数，改为使用RandomReal[]）
Max[a,b,c,...]，Min[a,b,c,…] a,b,c,…的极大/极小值

更新日志

wolfram mathematica v10.3
1、通过软件，访问 Wolfram 语言中大量的数学函数恒等式及其性质
2、新的地理计算功能，例如：TravelDirections、TravelDistance，以及更多用于旅程时间、方法和相关数据的计算
3、新的AnatomyData和AnatomicalStructure解释器类型，通过与 Wolfram Cloud 的连接进行计算和部署
4、对特定类型实体进行分组、复制以及识别的功能，从而实现更自动且有效的计算
5、支持随机矩阵分布和属性
6、用于测试表达式的比较运算符，例如：GreaterThan、LessThan以及EqualTo
7、增添了单词和字母字符串操作的语言学数据，强化了对自然语言的理解
8、新的日期和时间功能，用于表示和处理时区
9、支持符号式求解偏微分方程和特征问题
10、更多便捷的网络编程选项，可用于主机查询、IP 地址表示以及套接口连接
11、增强的文本元素和结构处理分析功能，包括定义、词性、翻译等
12、与GoogleCalendar、GoogleContacts和Yelp数据的新服务连接选项，以及用于学术研究的ArXiv和CrossRef
13、对核心 Wolfram 语言以及桌面和云端的 Wolfram 系统界面功能进行了众多改进